
Scientific Background
The study of fluid flow is a unique science that extends into the realm of pure mathematics. In fact, proof for a unique solution to the equations that govern turbulent flows has yet to be found.
In spite of the mathematical difficulty, all fluids (air, water, oil, pure gases, etc…) are simply governed by conservation of mass and momentum. However, applying these laws in this context gives rise to non-linearity, instability, and chaotic behaviour.
I think the vector form of these governing equations is most elegant, but if you’re not interested in math, feel free to skip these sections.
Conservation of mass states that fluids are continuous, and cannot be spontaneously created or destroyed.
If density changes with time ($\partial \rho / \partial t$), there must be some corresponding inflow or outflow of fluid mass ($\rho\textbf{u}$). $$ \frac{\partial \rho}{\partial t} + \nabla \cdot (\rho \textbf{u}) = 0$$
If we assume density is constant (incompressible flow), then conservation of mass is only dependent on inflows and outflows of fluid. Therefore, only velocity needs to be known to ensure mass conservation,
$$ \nabla \cdot \textbf{u} = 0$$
If you have a completely full tank of water with a tap above and no drain, turning on the tap must cause it to overflow. Anything that goes in, has to come out. A seemingly simple concept that has significant mathematical implications and sometimes non-intuitive effects.
The momentum change of a small fluid parcel in both time and space ($\frac{D}{D t}(\rho \textbf{u}$)) is equal to the stresses on that fluid parcel ($\boldsymbol{\sigma}$).
This is simply Newton’s second law in classical mechanics. If density is again assumed constant, we can re-write $\textbf{F}=m\textbf{a}$ (or more precisely $m\textbf{a}=\textbf{F}$) as,
$$ \begin{aligned} \rho\frac{D \textbf{u}}{D t} &= \nabla \cdot \boldsymbol{\sigma} + \rho \boldsymbol{g} \\ &= -\nabla p + \nabla \cdot \boldsymbol{\tau} + \rho \boldsymbol{g} \end{aligned} $$
Note, we separate the stress into pressure ($p$) and shear ($\boldsymbol{\tau}$), since the former is the primary quantity of interest, and the latter may be simplified with a model.
Pressure, by definition, is normal stress that results in purely elastic deformation. Most fluids do not resist elastic deformation, and consequently will flow with the direction of pressure gradients ($\nabla p$). However, fluids are subject to friction when interacting with a solid surface. Therefore, they tend to deform according to shear stresses induced by these solid surfaces. A fluids ability to resist this deformation is known as viscosity. Shear stresses may also be induced by differences in density within a fluid, or between two different fluids.
The Navier-Stokes equations are the most widely referenced shear stress model. They assume the fluid is Newtonian, which means the shear stresses ($\boldsymbol{\tau}$) are proportional to the rate of strain ($\nabla \textbf{u}$) by the viscosity ($\mu$).
$$ \rho\frac{D \textbf{u}}{D t} = -\nabla p + \nabla \cdot \mu\nabla\textbf{u} + \rho \boldsymbol{g} $$
Below is visual cartoon of momentum conservation (as I imagine it). Bear in mind, it is not a rigorously representative diagram.
Pressure acts as a normal stress that tends to change volume. Since volume is fixed by mass conservation, pressure causes a fluid to flow. Shear stresses are generated by friction at solid surfaces, causing the fluid to deform. The fluids ability to resist this deformation is known as viscosity
Since there isn’t an exact method to solve for fluid momentum, we resort to brute force approaches. Simulations can make thousands of guess-and-check iterations before the problem is solved. This is ultimately very inefficient (even with modern computers), and highly complex models are needed to approximate turbulence.
Experiments remain the best way to approach fluid flow problems, but engineers benefit greatly from simulations that help improve their designs and physical understanding.
My Research
I attended Queen’s University in Kingston, Ontario as a Master’s student starting in 2016. I completed my degree while simultaneously working at Ford in early 2019. During that time, I presented at an international conference, and published two papers.
Since I’ve graduated, several more papers have been published, and continue to be written based on my writings and research. I’m proud that my early research and experiments continue to be used for deeper learning!
The OTTER Lab
The OTTER lab facility at Queen’s University is where I performed all my experiments.
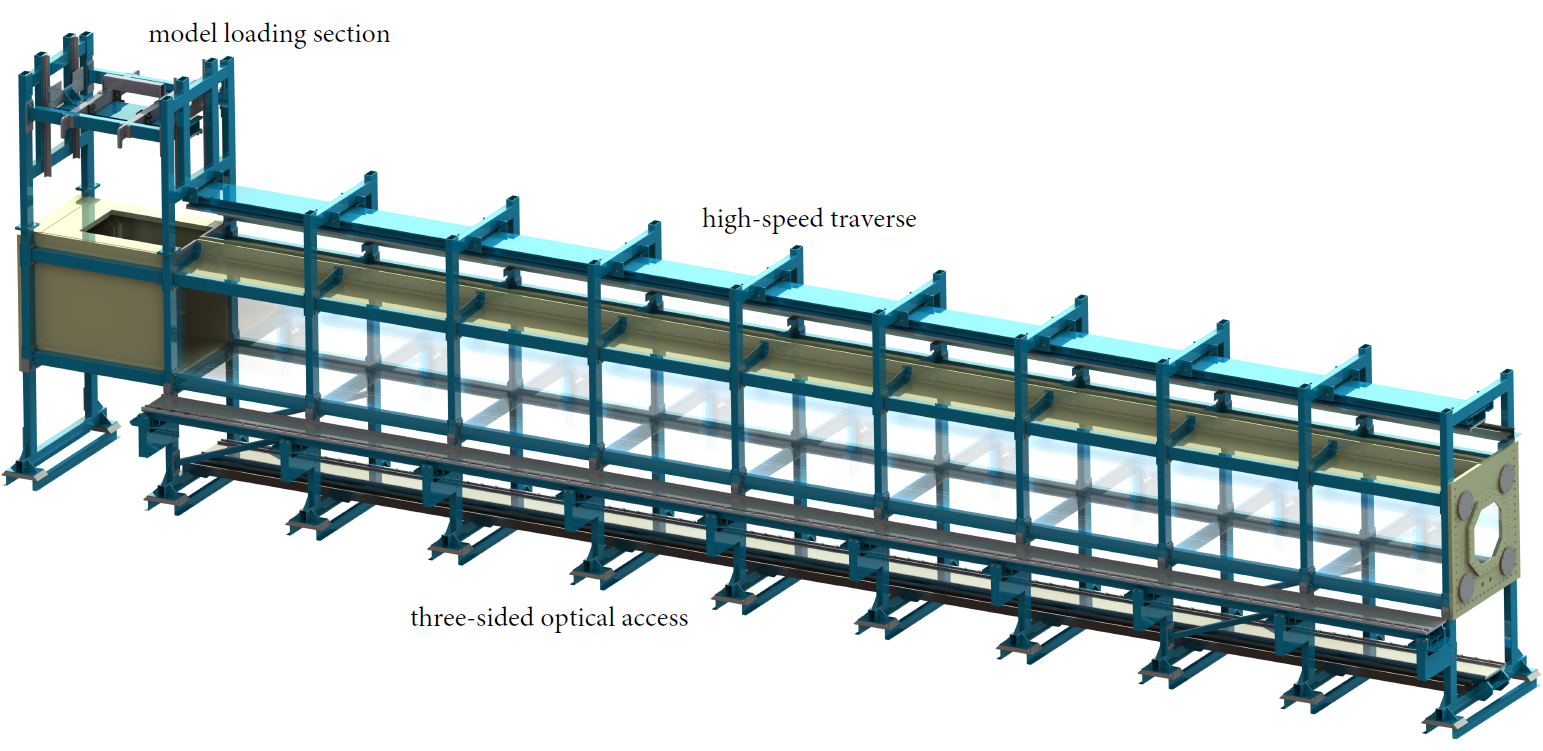
A towing tank uses a track to pull an object/model through stationary water (rather than using a fan to push the air/water around the model). It’s cross-section is 1 square meter (10.75 sq ft), and it is 15 meters (50 ft) long. The glass windows allow for optical measurements by laser and high speed camera.
The OTTER lab towing tank can pull a scaled down aerodynamic model through the water at up to 2 $m/s$. This is equivalent to about 65 mph for a similar sized scale model in air.
One of the biggest advantages of a towing tank, is the ability to easily accelerate the model in water with zero latent turbulence. For that reason, most of my research is centered around the aerodynamics of accelerating bodies.
Highlighted Publications
My first paper on accelerating delta wings.
My second paper was in collaboration with two other students. In this work, I performed the experiments, and wrote the results and conclusions sections (including the plotting and experimental analysis).
Other publications I’ve contributed to
Reconstruction of Turbulent Flows in Three Dimensions
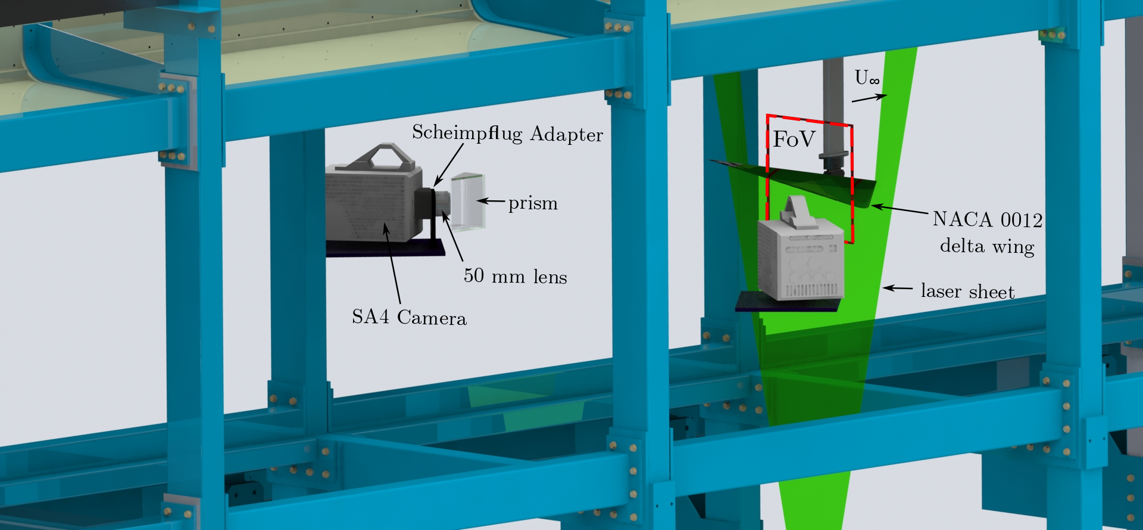
In these experiments, a model is passed through a plane of laser light. Two cameras record the motion of a particulate added to the water which get highlighted by the laser. A second camera allows for the stereoscopic effect to capture all three dimensions of flow velocity.
A 3D reconstruction of the stalled flow over a delta wing was generated using the ‘scanning’ method above. Renders of the fluid velocity it’s derivatives give deep insight into the structure of airflow over similarly shaped aircraft during stall.
The render above shows vorticity, which is a measure of the flows rotation. Vorticity in an important metric for understanding stall and losses due to friction.
Accelerating Bodies and Flows (Gusts)
Most practical aerodynamic analysis is performed with an object traveling at a constant speed (or a still object, with air at a constant speed). However, many natural swimmers and fliers operate based on principles of accelerating through air or water.
Birds constantly flap wings to fly and propel themselves through air. Various forms of marine life oscillate their fins to propel themselves through water. Often the maneuverability of these animals exceeds the engineering capability of our small-scale drones and submarines.
Another direct application of accelerating flows is gusts. Aircraft experience gusts during updrafts and cross winds on landing. My research was actually funded by the US Office of Naval Research, due to their interest in gust stability of autonomous combat aerial vehicles.
Lots of wind noise in this video, avoid headphones!
To study the effect of accelerating flows, a technique called particle image velocimetry may be used to track particulate suspended in water. A laser highlights the particulate, and high speed cameras track their motion.
Below, a sphere is accelerated from rest to different final velocities over the same distance. By studying how friction between the sphere surface and fluid generates turbulence, we gain a deeper understanding of drag forces.
Above is the raw footage recorded by the high speed cameras. Below is corresponding data post-processed. The data shows how friction generates flow structures during acceleration that ultimately form the steady-state wake.
Strong acceleration can even reverse a stall, and cause a wing to regain lift.
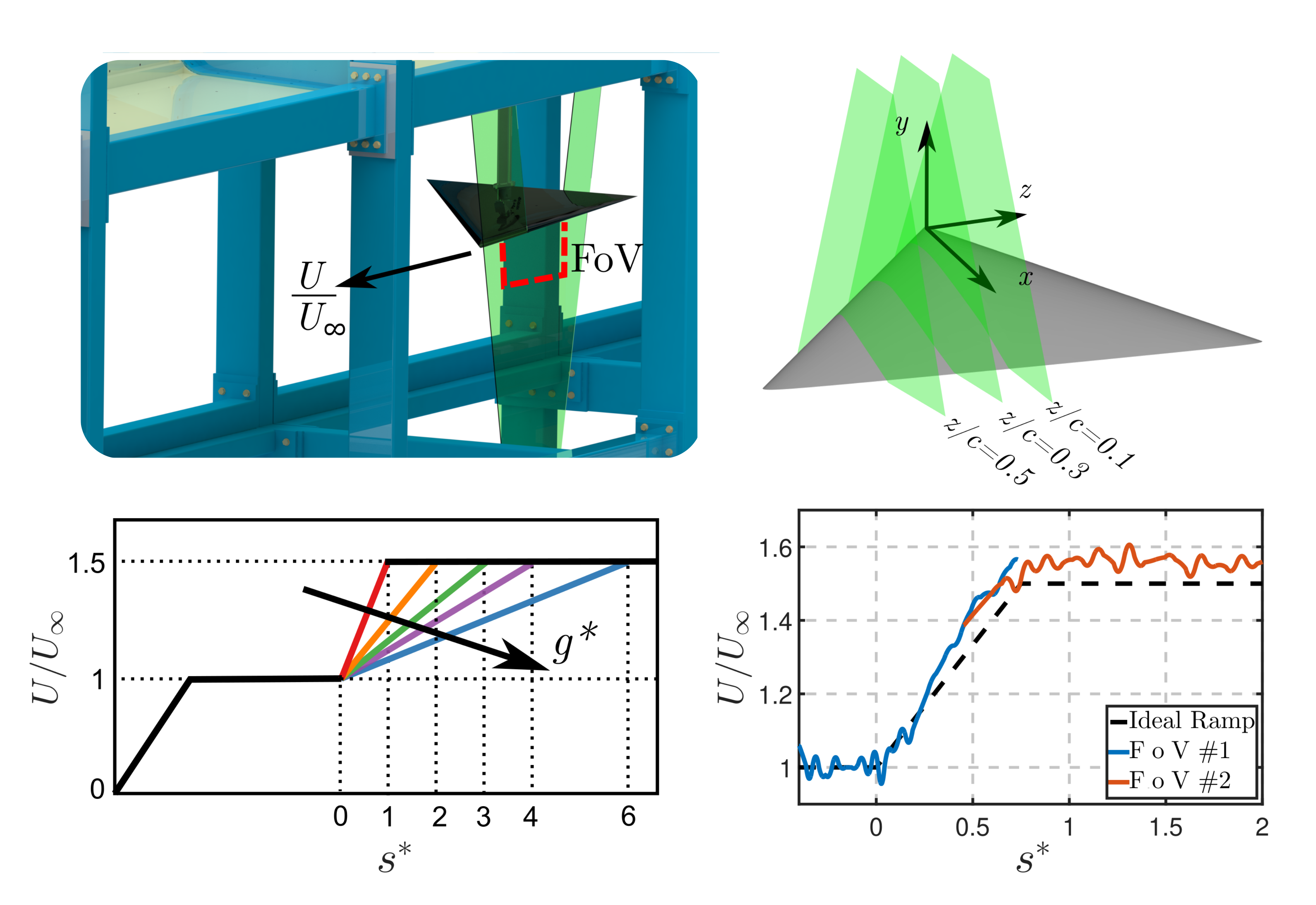
Below, you can see a pressure signature on the wing surface as it accelerates. Notice the strong load spikes that can upset the stability of the wing.
The video below shows the flow velocity that corresponds to the pressure fluctuations above. In the bottom row, the flow is initially ‘separated’ or stalled. The sudden acceleration causes the flow to reattach to the wing, resulting in a sudden spike in lift.
For any more questions on my research, feel free to reach out and contact me at the contact information on the homepage.